To exemplify this, imagine a 3d cube, which is bounded by 6 faces. Now, imagine that the cube is sliced into infinite squares, each one with the dimensions of a single face. The only faces bounding the cube that are important in this case are the front face (the one facing to the observer) and the back face, since they are also slices. If you rotate the cube, you are actually rotating these slices. This same method can be applied to 4d objects, except that instead of slicing the object into 2d faces, we are slicing the objects into 3d cells.
The Tesseract (Hypercube)
The tesseract is the 4d equivalent to the 3d cube, and is the more talked-about 4d object. However, many people don't seem to understand it, especially when seeing animations of a rotating hypercube. This section will demonstrate, through simple comparision with the 3d cube, how we can easily imagine a rotating hypercube, and how it is not so different than imagining a rotating 3d cube. Make sure you understand the Field of Vision section of the previous article before proceeding.
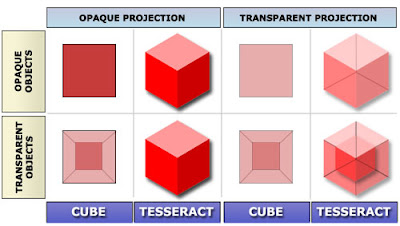
But first, let`s take a look at the 2d projection of a 3d cube. That looks just like an ordinary 3d cube drawn in a piece of paper. We (3d entities) can see up to 3 faces of the cube at same time, and we can see all the points of this projection at the same time as well. However, if this same projection was brought into a 2d world, 2d entities would only be able to see one "line" at a time: remember that they are also 2d shapes, and they would have to stay by the side of the 2d projection of the cube in order to see it (they can`t see the projection from the "front", like we can). So the only way for them to see all the points of this 2d projection at the same time, like us, would be to make this projection transparent. If the angle of the 3d cube is such that we can only see the front face, then the 2d projection will be a perfect square, and to be seen in a 2d world, it would be a transparent square.
Taking that analogy into the 4d tesseract, if the angle of the tesseract is such that 4d entities can only see the first cell (which is a 3d cube), then the 3d projection of the tesseract is merely a 3d cube. But in order for us to see all the points inside that cube, like 4d entities can, we have to make this projection transparent. So a transparent, 3d cube is the 3d projection of an opaque tesseract. Then, we can just project this transparent cube into 2d like we normally do.
But what about transparency? Well, if we look at a transparent 3d cube directly from the front, when the shape of its 2d projection is a square, we will see a big square with a small square in the middle, and four lines connecting the edges of both squares. The square in the middle is actually of the same size of the outer square, but because of depth, it looks smaller to the observer.
The same thing is true for the tesseract. When the transparent tesseract is being observed from the "front", the 3d projection will be a 3d cube with a smaller 3d cube in the center, and all their vertices will be connected. This is the most common image of the projected tesseract on the internet, but most people don't know that they are looking at a transparent tesseract, and not an opaque one. Notice that, the true 3d projection of a transparent tesseract would also be opaque, but in order for we to observe it, we make this projection transparent.
 |
If you understood the concept described above, then imagining the rotations of a tesseract won`t be so complicated. All you have to do is take the 2d projection of a rotating cube and transform it into a 3d shape. That will be the 3d projection of a rotating tesseract.
For example, imagine that you are looking at a transparent 3d cube from the front. The 2d projection will be a square with a smaller square inside. If you start rotating it, without ever changing the orientation of the top or bottom face, the small square in the middle will start to flatten and start "moving" to the side, and the outer square will flatten and go to the other side. At some point, one of the squares will look entirelly flat, like a line. Eventually, both squares will be actually on the "sides" of the cube, and the front face is now formed by a square that was previously on the side. Notice that, while the cube is rotating, the 3d projection is not a perfect square at all times, but only when just one of the faces is on the front.
The exact same thing happens to the tesseract. The 3d projection of a transparent tesseract, when only one of the cells is brought to the "front", is a large cube with a smaller cube in its center. As the tesseract is rotated, the smaller cube will start to flatten and move to one of the sides of the cube, and the outer cube will start to flatten and move to the other side. At one point, one of the cubes will look entirelly flat, like a square. Eventually both cubes will be actually on the sides of the tesseract, and the front cell of the cube is now formed by a cube that was previously on the side. Here, the 3d projection is also constantly changing shape, in a similar fashion to the 2d projection of the cube, and only at some points it forms a perfect 3d cube. With this method, is very simple to imagine a rotating tesseract.
 |
As you can see, "following" one of the 3d cubes (cells) of the rotating tesseract while it rotates is just like following one of the faces of a 3d cube rotating - the outer cube eventually becames the inner cube, and then becames the outer cube again. We can see up to four cells of the tesseract at the same time, depending on the angle it's being viewed from. Also notice that, just like the faces of the cube becames "reversed" when they are not in the front, the cells of the tesseract also becames reversed when they are not in the surface of the 3d projection. That means the content inside of the inner cube of the projection (for instance) is flipped horizontally.
Another thing worth pointing out is that 4d entities can assign a "front" and a "back" side to a 3d object. Depending on the angle the 4d object is being viewed from, it might look slightly or entirelly flat to a 4d entity. When a 3d object looks completely flat, only part of the surface of the object will be visible to the entity, and the rest of the surface, as well as all the points inside the object, will be hidden behind the surface, further away in the 4d direction. If the 3d object is only partially flat, all the points of the object will be visible, but the content will look skewed. This behavior can be observed on any of the cells that form the hypercube. Remember that when a 4d entity looks at a 3d object from the "back", the content of that object will appear reversed.
The Hypersphere
The hypersphere is the 4d equivalent of the 3d sphere, and is formed by several (infinite) 3d spheres, just like a 3d sphere is formed by infinite 2d circles.
Imagine a transparent 3d sphere that has been sliced into several 2d circles. The circle closest to you is very small, or almost a point. The circle in the middle of the sphere is the largest one. That is true even if you rotate the sphere clock-wise or counter clock-wise. Now, take one of these circles, one that is between the middle of the sphere and the circle closest to you. As you rotate the sphere, this circle will appear to flatten (from your position). At some point, this circle will appear to be a single line. In fact, at this point, all the circles will appear to be a line, but since there are an infinity of them, the projected image of the sphere will still be a circle.
When a 4d entity looks at the hypersphere from the "front" (no matter what the 3d angle of the projection is), then the 3d sphere closer to the observer will be situated exactly in the center of the projected sphere. In reality, though, it would be very small, like a point. If the hyphersphere is transparent, then the 3d sphere further from the observer will also be visible, and due to dept, it will appear to be smaller than the nearest sphere.
The largest 3d sphere that forms the hyphersphere will compose the surface of the projected 3d sphere, if the hyphersphere is opaque, much like the largest circle of a 3d sphere would be its contour. If it is transparent, then all the points inside the largest sphere will be visible, as well as all the points inside all 3d spheres.
As the hyphersphere is rotated across the 4th dimension, these imaginary sphere-shaped crossections will start to "flatten" and "move" to the sides. Just imagine a 3d sphere being rotated, and the circles that compose it will have the same mentioned behavior. However, instead of flattening a circle until it becames a line, we are flattening an actual 3d sphere until it becames a circle. Notice that at all times the shape of the projection is still a sphere. Even when looking at a hypersphere from the "side", all the circles that constitute it will compose a 3d sphere.
0 comments:
Post a Comment